E aí, galera! Bora falar de um dos teoremas mais famosos e cobrados da matemática: o Teorema de Pitágoras. Esse teorema é praticamente a estrela das provas, vestibulares e questões do IF. Mas, afinal, o que ele diz e onde realmente podemos aplicá-lo? A primeira coisa que você precisa saber é que o Teorema de Pitágoras só se aplica a triângulos retângulos, como o da figura a seguir:
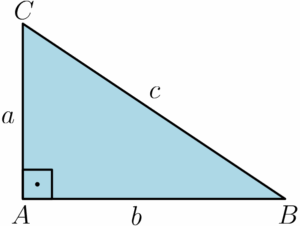
Nota: Um triângulo retângulo é um triângulo que possui um ângulo de $90^circ$.
Na figura acima, as letras maiúsculas A, B e C representam os vértices do triângulo, e as letras minúsculas a, b e c representam os lados do triângulo. Perceba que o triângulo $ABC$ é retângulo no vértice A. Esses lados, $a$, $b$ e $c$, possuem nomes especiais, que precisamos conhecer para enunciar o Teorema de Pitágoras. Os lados $a$ e $b$ são chamados de catetos, enquanto o lado $c$ é chamado de hipotenusa, sendo o maior lado e sempre oposto ao ângulo reto (ângulo de $90^circ$), conforme ilustrado na figura:
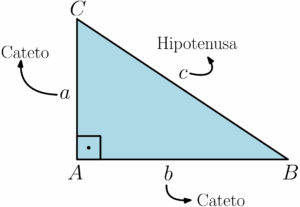
Muitos alunos têm dificuldade em identificar a hipotenusa quando a figura está rotacionada, mas não se preocupe: a chave é sempre olhar para o lado oposto ao ângulo de $90^circ$ graus. Não importa como o triângulo esteja posicionado, esse lado será sempre a hipotenusa:
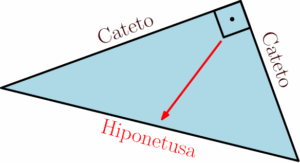
Agora que entendemos como identificar os lados de um triângulo retângulo, podemos enunciar o nosso querido teorema:
Teorema de pitágoras: O quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Traduzindo esse enunciado para expressões matemáticas, com base na segunda figura que vimos, temos a seguinte equação:
$$c^2=a^2+b^2$$
Interpretação visual
O Teorema de Pitágoras tem uma representação visual muito interessante. Considere um triângulo retângulo de lados $a$, $b$ e $c$:
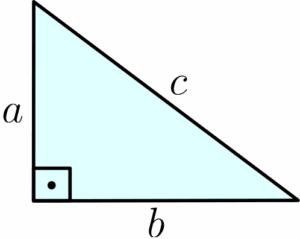
Se pegarmos cada lado desse triângulo e elevá-los ao quadrado, formaremos três quadrados, de lados $a$, $b$ e $c$, cujas áreas são dadas, respectivamente, por $a^2$, $b^2$ e $c^2$, veja a figura:
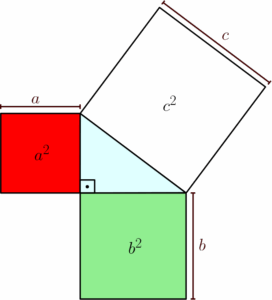
Se fatiarmos os dois quadrados menores, que são dados pelos quadrados dos catetos, teremos a seguinte figura:
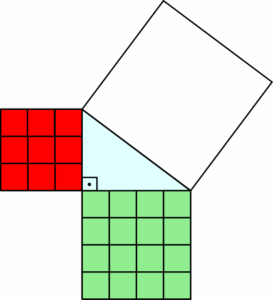
Isso é exatamente a interpretação geométrica do Teorema de Pitágoras: a soma das áreas dos quadrados construídos sobre os catetos é igual à área do quadrado construído sobre a hipotenusa. Por isso, os recortes dos quadrados menores se encaixam perfeitamente dentro do quadrado maior.
Isso cai em prova, professor? Sim! Veja essa questão do IFFarroupilha:
Questão 1 (IFFarroupilha): A figura a seguir apresenta três quadrados e um triângulo em que seus lados são representados pelas letras $a$, $b$ e $c$. Uma relação matemática fundamental que expressa a igualdade entre a soma das áreas dos quadrados menores com o maior é:
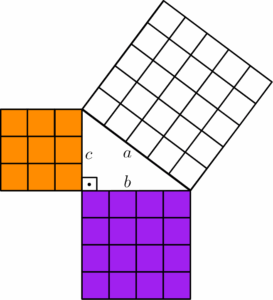
a) a fórmula de Báskhara.
b) o teorema de Pitágoras.
c) o teorema de Tales.
d) um conjunto numérico.
e) um polígono convexo.
Solução: Como você acompanha o helpIF, com certeza marcou a letra b, não é mesmo? Isso se deve ao fato de que, como vimos anteriormente, o Teorema de Pitágoras expressa exatamente essa igualdade: a soma das áreas dos quadrados construídos sobre os catetos é igual à área do quadrado construído sobre a hipotenusa.
Além dessa aplicação geométrica, nas provas dos IFs, também são cobradas questões que pedem para encontrar um dos lados do triângulo retângulo, como veremos adiante.
Como aplicar o Teorema de Pitágoras?
A grande vantagem desse teorema é que, sempre que nos deparamos com um triângulo retângulo e conhecemos as medidas de dois de seus lados, podemos utilizar o teorema para encontrar o valor do terceiro lado, seja ele a hipotenusa ou um dos catetos. Vejamos um exemplo:
Exemplo 1: Em um triângulo retângulo, se os catetos medem $3$ e $4$ unidades, qual é o comprimento da hipotenusa?
Solução: A figura que representa a situação acima é a seguinte:
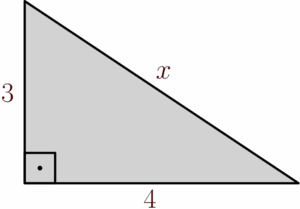
Desejamos determinar o comprimento da hipotenusa, que denotamos por $x$, os valores dos catetos foram dados no enunciado, agora podemos aplicar o Teorema de Pitágoras:
$$x^2=3^2+4^2$$
Agora basta resolver a equação isolando o valor de $x$:
$$x^2=9+16$$
$$x^2=25$$
$$x=sqrt{25}$$
$$x= pm 5$$
já que não existem medidas de comprimento negativas, consideraremos apenas a solução positiva. Assim, concluímos que:
$$x=5$$
Agora vejamos um exemplo onde precisamos encontrar um dos catetos:
Exemplo 2: Em um triângulo retângulo, se a hipotenusa mede 10 unidades e um dos catetos mede 6 unidades, qual é o comprimento do outro cateto?
Solução: Desta vez não irei usar desenhar a figura. Partimos diretamente para a aplicação do teorema. Sabemos que a hipotenusa mede $10$ unidades e um dos catetos mede $6$ unidades. Denotamos o outro cateto por $ x $. Aplicando o Teorema de Pitágoras:
$$10^2=6^2+x^2$$
Agora basta resolver a equação isolando o valor de $x$:
$$100=36+x^2$$
$$x^2=100-36$$
$$x^2=64$$
$$x=sqrt{64}$$
Consideraremos apenas a solução positiva pelo mesmo motivo do Exemplo 1:
$$x= 8$$
Esse é o poder do Teorema de Pitágoras: dados dois lados de um triângulo retângulo, podemos sempre encontrar o terceiro. Legal, né? Mas não é só isso! Também podemos usar a recíproca desse teorema, que nada mais é do que a ideia oposta. Ou seja, se você tem um triângulo e verifica que a soma dos quadrados de dois lados é igual ao quadrado do terceiro, então esse triângulo é necessariamente retângulo, e o ângulo oposto ao maior lado (hipotenusa) vai ser o angulo reto. Vejamos um exemplo:
Exemplo 3: Dado um triângulo de medidas $3$, $4$ e $6$, verifique se o triângulo é retângulo.
Solução:Como a maior medida é 6, se esse triângulo for retângulo, ele tem que ter 6 como hipotenusa e os outros lados como catetos. Vamos aplicar o teorema de Pitágoras:
$$6^2 = 3^2 + 4^2$$
$$36 = 9 + 16$$
$$36 = 25$$
Perceba que chegamos a uma coisa que não é verdade, $36$ não é igual a $25$. Portanto, esse triângulo com lados $3$, $4$ e $6$ não é retângulo.
Desafio: Suponha que não tivéssemos a informação de que os triângulos dos Exemplos 1 e 2 são retângulos, mas que fossem dados os valores encontrados nas respostas para os exemplos. Mostre que eles são retângulos utilizando a ideia apresentada acima.
Teorema de Pitágoras nas questões dos Institutos Federais
As questões cobradas nos Institutos Federais sobre este teorema são diversas. Haverá aquelas em que será possível aplicar diretamente o Teorema de Pitágoras, outras que não são exatamente questões desse teorema, mas em que você pode utilizá-lo para ajudar a resolver. Enfim, é uma grande diversidade de questões. Por isso, aqui trabalharemos com três questões de IFs para praticar o que aprendemos, mas haverá um artigo dedicado à resolução de questões dos IFs utilizando o Teorema de Pitágoras. Caso queira ver resoluções de questões em vídeo, recomendamos nosso canal clique aqui.
Questão 1 (IFFar): Na figura a seguir, os lados do triângulo são medidos em metros.
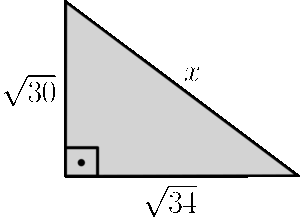
Qual é o valor do segmento $x$?
a) 4 m.
b) 5 m.
c) 6 m.
d) 7 m.
e) 8 m.
Solução: Vamos lá, note que o triângulo que está na figura é retângulo, pois tem um ângulo de $90$ graus indicado. Como temos o valor de dois lados, podemos encontrar o terceiro usando nosso querido Teorema de Pitágoras. O lado que está oposto ao ângulo reto é o lado $x$, ou seja é nossa hipotenusa, os outros dois lados serão os catetos: $sqrt{30}$ e $sqrt{34}$. Vamos para a aplicação do teorema:
$$x^2=(sqrt{30})^2+(sqrt{34})^2$$
Como temos uma raizes quadradas elevadas a um expoente $2$, que são operações inversas uma da outra (potenciação/radiciação), a raiz quadrada é “cortada” junto com o expoente 2, portanto:
$$x^2=30+34$$
$$x^2=64$$
$$x=sqrt{64}$$
$$x= 8$$
Logo, $x$ vale $8$, alternativa correta letra e.
Questão 2 (IFMA): A Figura 1 mostra uma área de desmatamento na região Amazônica em forma de um triângulo retângulo. Sabe-se que as medidas $AB$ e $BC$ são, respectivamente, $8$ e $10$ metros.

A medida, em metros, do segmento $AC$ é
a) 13.
b) 9.
c) 6.
d) 12.
Solução: Mais um problema clássico de Teorema de Pitágoras. Temos o valor do comprimento de dois lados: o segmento $AB = 8$ e $BC = 10$. Note que o segmento $BC$ está oposto ao ângulo de $90^circ$, portanto, ele é nossa hipotenusa. O que queremos encontrar é o segmento $AC$, que é um cateto. Chamaremos esse segmento de $x$ para facilitar a escrita. Vamos aplicar o teorema:
$$10^2=8^2+x^2$$
$$100=64+x^2$$
$$x^2=100-64$$
$$x^2=36$$
$$x= sqrt{36}$$
$$x = 6$$
Deste modo, o comprimento do segmento $AC$ é $6$ metros, alternativa c.
Questão 3 (IFRN): Um guarda florestal responsável por fiscalizar uma determinada área de preservação ambiental identificou as medidas dos lados $AC$ e $BC$ do triângulo retângulo $ABC$, como também o ponto $A$, considerando-o o ponto mais alto de uma determinada árvore, de acordo com a Figura 3. Sabendo que o guarda florestal, tem, aproximadamente, $1 ,68$ m de altura, a medida, em metros, da altura da árvore é de
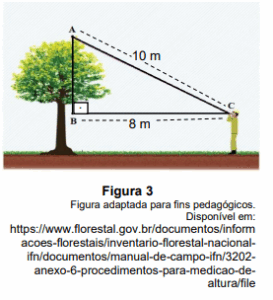
A medida, em metros, do segmento $AC$ é
a) 6,0.
b) 6,86.
c) 7,68.
d) 7,0.
Solução: Queremos encontrar a altura da árvore com base nessa figura. Esse problema já nos requer um pouco mais de atenção, percebemos na figura claramente um triângulo $ABC$ retângulo, como o próprio enunciado nos afirma. O lado oposto ao ângulo reto, que é o segmento $AC$, mede $10$ m, que é nossa hipotenusa. Um dos catetos, que é o segmento $BC$, vale $8$ m, e o outro segmento $AB$ não sabemos. Para encontrar a altura da árvore, precisamos saber esse segmento $AB$, pois a altura da árvore pode ser encontrada somando o valor do segmento $AB$ com a altura do guarda. Veja a situação:
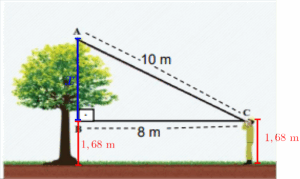
Então, vamos focar em encontrar o valor do segmento $AB$, que chamaremos de $x$, e para encontrá-lo, podemos aplicar o teorema de Pitágoras:
$$10^2 = x^2 + 8^2$$
$$100 = x^2 + 64$$
$$100 = x^2 + 64$$
$$x^2 = 100 – 64$$
$$x^2 = 36$$
$$x = sqrt{36}$$
$$x = 6$$
Lembrando novamente, consideramos apenas a solução positiva, pois não existe medida de comprimento negativa. Pronto, achamos $x = 6$. Basta marcar a letra $a$, né, professor? Errado! Lembre-se que o enunciado está pedindo a altura da árvore. Esse $x$ que encontramos é o segmento $AB$. A altura da árvore é dada pela soma do segmento $AB$ (que chamamos de $x$) com a altura do guarda florestal, que é $1,68$ m. Então, a altura da árvore vai ser dada por:
$$x + 1,68$$
Como encontramos $x = 6$, temos:
$$6 + 1,68 = 7,68$$
Agora sim, achamos a altura da árvore, e a letra c é a correta.
Teorema de Pitágoras em vídeo
Caso queria assistir um vídeo sobre a teoria do Teorema de Pitágoras, clique no vídeo abaixo:
https://www.youtube.com/watch?v=TpEEzHNrHh4
E para resoluções de questões clique nos vídeos abaixo:
https://www.youtube.com/watch?v=37Wfsuz_hZshttps://www.youtube.com/watch?v=ZNO9YBG5xa4https://www.youtube.com/watch?v=o5QSoHAW_wY&t=1086s
Demonstração do Teorema de Pitágoras
Atenção: esta parte do nosso estudo é destinada àqueles curiosos que desejam entender como podemos chegar na relação $c^2 = a^2 + b^2$ apresentada anteriormente. Embora não seja obrigatória para a sua preparação para a prova do $IF$, achei importante incluí-la para mostrar que toda ”fórmula” matemática tem uma explicação e uma forma de se chegar nelas.
Se a sua rotina de estudos estiver muito apertada e o tempo for curto, sugiro que pule esta parte. Quando tiver um momento mais tranquilo, volte a ela e tente entender. Essas demonstrações podem te ajudar a aprimorar sua habilidade de raciocínio lógico e a forma como você encara os problemas.
Existem várias formas de se chegar à relação de Pitágoras. Abordarei aqui a que considero mais tranquila, que é usando as fórmulas de áreas de algumas figuras planas. Vamos, inicialmente, começar com um triângulo retângulo de lados $a$, $b$ e $c$, sendo $c$ a hipotenusa:
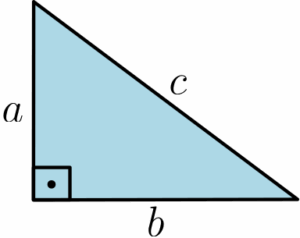
Agora, vamos pegar mais 3 triângulos idênticos a esse e posicioná-los de modo que possamos formar um quadrado de lado $a + b$:

Temos duas formas de calcular a área desse quadrado grande (de lado $a+b$) a primeira é usando o lado ao quadrado, ou seja:
$$A = (a + b)^2$$Esse $A$
representa a área do quadrado maior. Agora, desenvolvendo esse produto notável, teremos:
$$A = a^2 + 2ab + b^2$$
A segunda forma de calcular a área do quadrado grande é somando a área dos 4 triângulos retângulos e a área do quadrado menor de lado $c$, que está na cor branca no meio da figura. Logo, a área do quadrado maior também pode ser encontrada fazendo:
$$A = 4T + Q$$
onde $T$ é a área de um desses triângulo, por isso está multiplicado por 4, pois temos 4 triângulos, e $Q$ é a área do quadrado menor de lado $c$. Vamos primeiro encontrar a área de um triângulo, que é dada por:
$$T = frac{b cdot a}{2}$$
onde $b$ é a base e $a$ a altura, que também pode ser escrito como
$$T = frac{a cdot b}{2}$$
que é a mesma coisa, pois a ordem dos fatores não altera o produto, como dizia a professora Helena. A área do quadrado menor de lado $c$ é dada por:
$$Q = c^2$$
agora, substituindo esses resultados em $A = 4T + Q$, temos:
$$A = 4 cdot frac{a cdot b}{2} + c^2$$
simplificando:
$$A = 2ab + c^2$$
Lembra que, lá em cima, essa mesma área $A$ também poderia ser encontrada usando $A = a^2 + 2ab + b^2$? Então, podemos igualar esses dois lados da equação, pois ambos representam a mesma área:
$$2ab + c^2 = a^2 + 2ab + b^2$$
agora, organizando essa expressão, colocando o $2ab$ para o lado esquerdo, temos:
$$2ab – 2ab + c^2 = a^2 + b^2$$
uma coisa menos ela mesma é igual a zero, logo $2ab – 2ab$ é zero. Portanto, teremos:
$$c^2 = a^2 + b^2$$
que é o nosso querido e famoso Teorema de Pitágoras.
[baixar_material]